Modern computers come in all shapes and sizes, and they aid us in a million different types of tasks ranging from the serious, like air traffic control and cancer research, to the not-so-serious, like computer gaming and photograph retouching. But as diverse as computers are in their outward forms and in the uses to which they’re put, they’re all amazingly similar in basic function.
At the heart of the modern computer is the microprocessor a tiny, square sliver of silicon that’s etched with a microscopic network of gates (Transistors) and channels (wires or lines) through which electricity flows.
The microprocessor isn’t just the “heart” of a modern computer—it’s a computer in and of itself. Once you understand how this tiny computer works, you’ll have a thorough grasp of the fundamental concepts that underlie all of modern computing systems.
The Calculator Model of Computing
Below figure is an abstract graphical representation of what a computer does. In a nutshell, a computer takes a stream of instructions (code) and a stream of data as input, and it produces a stream of results as output.
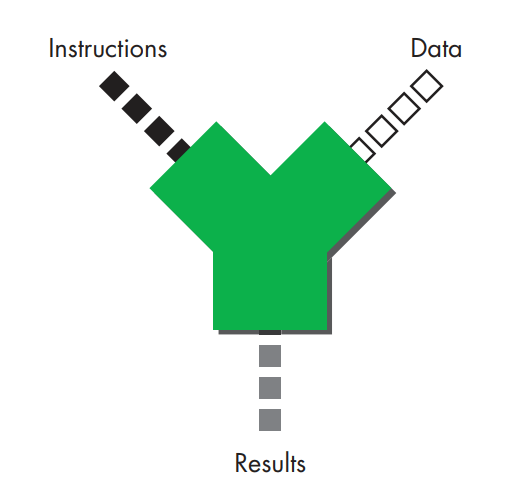
Let's consider the code stream consists of different types of arithmetic operations and the data stream consists of the data on which those operations operate. The results stream, then, is made up of the results of these operations. You could also say that the results stream begins to flow when the operators in the code stream are carried out on the operands in the data stream.
To illustrate this point, imagine that one of those little black boxes in the code stream is an addition operator (+) and that two of the white data boxes contain two integers to be added together.

You might think of these black-and-white boxes as the keys on a calculator with the white keys being numbers and the black keys being operators, the gray boxes are the results that appear on the calculator’s screen.
Thus, the two input streams (code and data) represent sequences of key presses, while the output stream represents the resulting sequence of numbers displayed on the calculator’s screen.
The kind of simple calculation represents the sort of thing that we intuitively think computers do.
Like a pocket calculator, the computer takes numbers and arithmetic operators (such as +, –, ÷, ×, etc.) as input, performs the requested operation, and then displays the results. These results might be in the form of pixel values that make up a rendered scene in a computer game, or they might be dollar values in a financial spreadsheet.
The File-Clerk Model of Computing
The “calculator” model of computing, while useful in many respects, isn’t the only or even the best way to think about what computers do. As an alternative, consider the following definition of a computer:
A computer is a device that shuffles numbers around from place to place, reading, writing, erasing, and rewriting different numbers in different locations according to a set of inputs, a fixed set of rules for processing those inputs, and the prior history of all the inputs that the computer has seen since it was last reset, until a predefined set of criteria are met that cause the computer to halt.
In the file-clerk model, the computer accesses a large (theoretically infinite) store of sequentially arranged numbers for the purpose of altering that store to achieve a desired result. Once this desired result is achieved, the computer halts so that the now-modified store of numbers can be read and interpreted by humans.
This way of looking at computers is powerful because it emphasizes the end product of computation rather than the computation itself. After all, the purpose of computers isn’t just to compute in the abstract, but to produce usable results from a given data set.
In other words, what matters in computing is not that you did some math, but that you started with a body of numbers, applied a sequence of operations to it, and got a body of results. Those results could, again, represent pixel values for a rendered scene or an environmental snapshot in a weather simulation.
In a nutshell, a computer is a device that reads, modifies, and writes sequences of numbers. These three functions—read, modify, and write— are the three most fundamental functions that a computer performs, and all of the machine’s components are designed to aid in carrying them out.
The Stored-Program Computer
All computers consist of at least three fundamental types of structures needed to carry out the read-modify-write sequence:
Storage
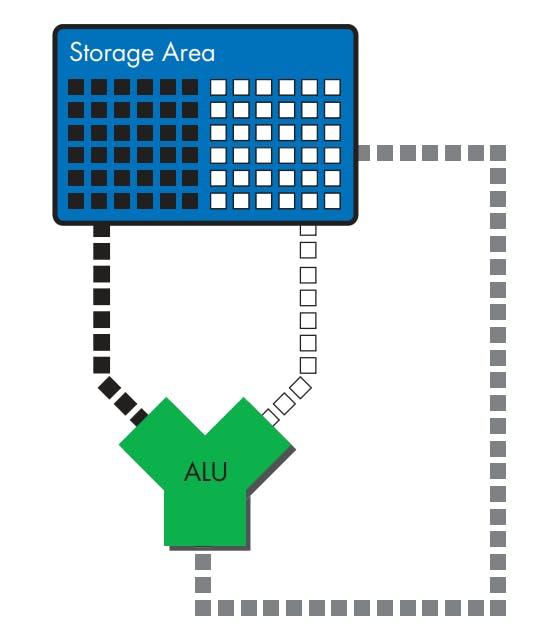
To say that a computer “reads” and “writes” numbers implies that there is at least one number-holding structure that it reads from and writes to. All computers have a place to put numbers (a storage area that can be read from and written to).
Arithmetic logic unit (ALU)
Similarly, to say that a computer “modifies” numbers implies that the computer contains a device for performing operations on numbers. This device is the ALU, and it’s the part of the computer that performs arithmetic and logical operations on numbers from the storage area.
First, numbers are read from storage into the ALU’s data input port.
Once inside the ALU, they’re modified by means of an arithmetic calculation.
Then they’re written back to storage via the ALU’s output port.
Bus
In order to move numbers between the ALU and storage, some means of transmitting numbers is required. Thus, the ALU reads from and writes to the data storage area by means of the Data Bus, which is a network of transmission lines for shuttling numbers around inside the computer. As well, Instructions travel into the ALU via the Instruction Bus.
.
The data stream is stored in a special storage area. Also, the code stream (as a prerecorded list of instructions) is stored in a special storage area.
The modern computer’s ability to store and reuse prerecorded sequences of commands makes it fundamentally different from the simpler calculating machines that preceded it.
Prior to the invention of the first stored-program computer,1 all computing devices, from the abacus to the earliest electronic computing machines, had to be manipulated by an operator or group of operators who manually entered a particular sequence of commands each time they wanted to make a particular calculation. In contrast, modern computers store and reuse such command sequences, and as such they have a level of flexibility and usefulness that sets them apart from everything that has come before.
Refining the File-Clerk Model
Let’s take a closer look at the relationship between the code, data, and results streams by means of a quick example. In this example, the code stream consists of a single instruction, an add, which tells the ALU to add two numbers together.
The add instruction travels from code storage to the ALU. For now, let’s not concern ourselves with how the instruction gets from code storage to the ALU; let’s just assume that it shows up at the ALU’s code input port announcing that there is an addition to be carried out immediately. The ALU goes through the following sequence of steps:
Obtain the two numbers to be added (the input operands) from data storage.
Add the numbers.
Place the results back into data storage.
The preceding example probably sounds simple, but it conveys the basic manner in which computers operate. Computers are fed a sequence of instructions one by one, and in order to execute them, the computer must first obtain the necessary data, then perform the calculation specified by the instruction, and finally write the result into a place where the end user can find it.
Those three steps are carried out billions of times per second on a modern CPU, again and again and again. It’s only because the computer executes these steps so rapidly that it is able to present the illusion that something much more conceptually complex is going on.
To return to our file-clerk analogy, a computer is like a file clerk who sits at his desk all day waiting for messages from his boss. Eventually, the boss sends him a message telling him to perform a calculation on a pair of numbers. The message tells him which calculation to perform, and where in his personal filing cabinet the necessary numbers are located. So the clerk first retrieves the numbers from his filing cabinet, then performs the calculation, and finally places the results back into the filing cabinet. It’s a boring, mindless, repetitive task that’s repeated endlessly, day in and day out, which is precisely why we’ve invented a machine that can do it efficiently and not complain.